对称二叉树的判断及二叉树的迭代遍历

发布: 2022-03-17 分类: 学习评论次数：阅读次数：本文字数： 2.4k

最近的我，感觉出了点问题（或许说我原本就是这么的菜。。）。为什么这么说呢？起因是这样的，今天呢，我终于开始刷leetcode的第101题了，不是有句话说得好嘛，万事开头难，对我而言，好像leetcode上的都是开头，怎么说呢，第101题标注的是一道简单题，题目的内容也就是这篇文章的标题——对称二叉树的判断。本来呢，这在人眼看来，也就是一件小case。只需要判断是不是对称的而已，不是很简单嘛，而且也标注的是简单题～可是呢，到我这，呵呵，硬是没想到正确的方向，一直在自己的“死胡同”里打转，待会就介绍下我的死胡同之旅（虽然也不算是死胡同）。

一碰到二叉树和图，我就有点小害怕，为啥呢，因为可以有很多变化～所以今天我就把二叉树的几种遍历（特指迭代）好好整理下。

题目介绍

1	给你一个二叉树的根节点 root ，检查它是否轴对称。

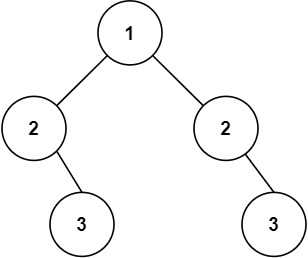
1 2	输入：root = [1,2,2,null,3,null,3] 输出：false

我的思路

我的思路很直接，相信一说，大家就懂了，但是呢，先说下，我的思路是错的。

我一开始想的是，既然和对称有关，那第一想到的就是回文数串，回文数串就是一个对称的经典实例。也正是这个想法，彻底地把我带进了深坑～

因此，我就想，既然都是对称，那对二叉树的某种遍历得到的序列是不是也是一个回文数串呢？而遍历的算法，先序与后序很明显是不符合要求的（对称），于是我兴高采烈地拿了几棵对称的二叉树用中序遍历进行实验，额，偏偏还都是回文数串，嗯，没错，，我信了，我竟然就这么相信：只要中序遍历得到的是一个回文数串，那一定是对称二叉树（错的❌）待会我会举出反例（其实是leetcode给出的。。）

思路既然都有了，我就开始写咯，于是，下面的这个代码就是最后的结果（期间，因为对null节点处理不当，导致错的原因很明显）

List<Integer> path = new ArrayList<>();
public boolean isSymmetric(TreeNode root) {
    if(root == null){
        return true;
    }
    Inorder(root);
    return isPalindrome();
}

private void Inorder(TreeNode root){
    if(root == null){
        path.add(null);
    }else if(root.left != null || root.right != null){
        Inorder(root.left);
        path.add(root.val);
        Inorder(root.right);
    }else{
        path.add(root.val);
    }
}

//判读回文
private boolean isPalindrome(){
    int i = 0;
    int j = path.size() - 1;

    while (i < j){
        if(path.get(i) == path.get(j)){
            i++;
            j--;
        }else{
            return false;
        }
    }
    return true;
}

结果是咋样的呢？

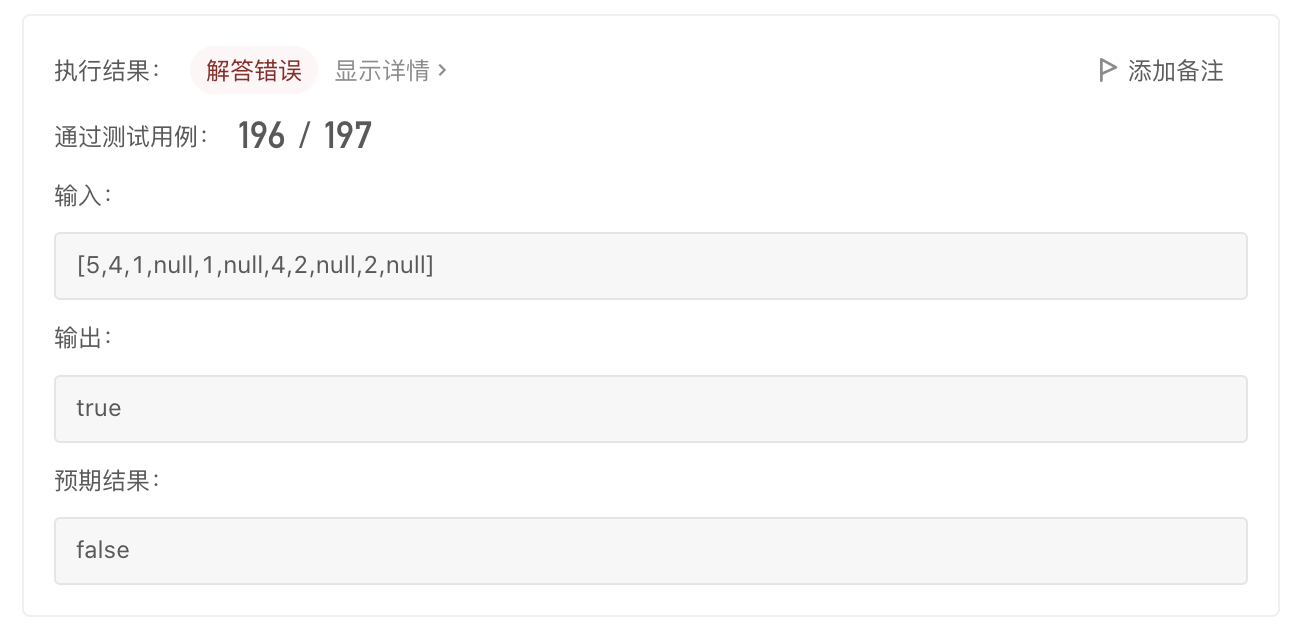
当时的我，都惊了，为啥会有一个过不去呢？于是我去把这个给的用例的二叉树画了个图看了下，就一切都明了了。。

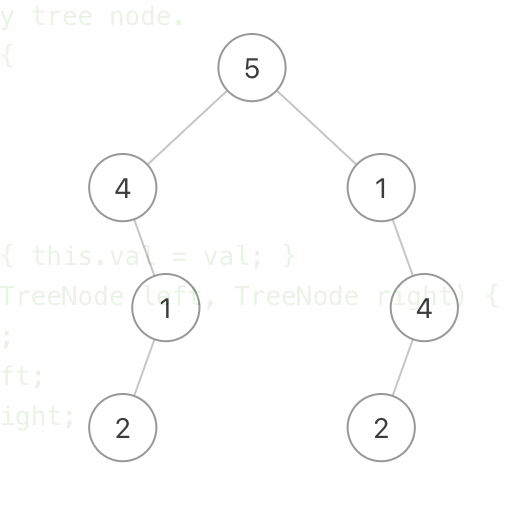
我相信只要是个正常人，一眼就能看出，这不是一个对称的二叉树。。可是为什么代码会将其认定为是对称的呢，我按照代码的思路，对它进行了一次中序遍历，结果发现，竟然是一个回文的数串。

经过了很长的思考，我想明白了，原来我一开始依靠的那个想法是不对的：

中序遍历得到的序列如果是对称的话，二叉树也是对称的（❌）

二叉树是对称的话，其中序遍历得到的序列一定是对称的（✅）

就这样，我被这道简单题弄的蛮难受的～

正确思路

相信很多人都明白镜像的道理，将一棵二叉树和其在镜中的二叉树相比较会发现，镜中的某个节点的左子树与镜外的对应节点的右子树是对称的，同样的，镜里的节点的右子树与镜外的对应节点的左子树是对称的，因此，如果使用递归来写，其实，只需要知道这个思路，还是很好写的，这也是为什么这道题会被标注为简单题的原因吧～

思路如下：

对于两棵树而言，镜像对称需要满足：

根节点的值相等
每棵树的左子树都与另一棵树的右子树互为镜像对称

//递归
public boolean isSymmetric(TreeNode root){
    return check(root, root);
}

private boolean check(TreeNode left, TreeNode right){
    if(left == null && right == null){
        return true;
    }else if(left != null && right != null){
        return left.val == right.val && check(left.left, right.right) && check(left.right, right.left);
    }else{
        return false;
    }
}

上面的解法呢，是递归的写法，那如果是迭代呢，众所周知，如果想把递归改成迭代，栈或者具有栈功能的其他数据结构是不可缺少的，当然，有时候会因为某些原因（比如访问顺序），而用队列来代替栈的使用，因此这道题也是如此。

思路上其实是没什么区别的，我们需要一个队列来存储节点。首先我们将树的根节点入队两次，然后再依次出队两个节点x，y（开始时自然是根节点），判断节点的值是否相等。

相等：分别将x的左节点（其实是左子树），y的右节点，x的右节点，y的左节点依次入队
不等：直接返回false

注意：红色部分的入队顺序是有讲究的，我们需要保证出队时连续两个节点在原二叉树中是对称的位置上。

//迭代
public boolean isSymmetric(TreeNode root){
    return check(root, root);
}

private boolean check(TreeNode root1, TreeNode root2){
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root1);
    queue.offer(root2);

    while (!queue.isEmpty()){
        root1 = queue.poll();
        root2 = queue.poll();
        if(root1 == null && root2 == null){
            continue;
        }
        if(root1 == null || root2 == null || root1.val != root2.val){
            return false;
        }

        queue.offer(root1.left);
        queue.offer(root2.right);
        queue.offer(root1.right);
        queue.offer(root2.left);

    }
    return true;
}

提示：由于LinkedList实现了Queue的某些方法，因此可以直接使用LinkedList；其次，使用queue的offer与poll方法可以避免某些异常的抛出。

二叉树的迭代遍历

二叉树的遍历方式有很多种，今天我为以后的自己整理四种出来：先序，中序，后序，层次。

其中，如果要我说的话，先序与后序相比较而言，简单点～

一般来说，不是后序很难嘛，为啥这里会说简单呢，因为如果是严格地按照后序来推，确实蛮难，但是，后序与先序之间的遍历是有关系的，至于是什么关系，待会再说～

先序遍历

处理顺序：中左右

遍历方法：将根节点入栈；出栈；访问，并将出栈的节点的右节点，左节点（因为要先访问左子树再访问右子树，加上栈的性质）依次入栈；以此类推下去即可

private void PreOrder(TreeNode root){
    Deque<TreeNode> stack = new ArrayDeque<>();
    stack.addFirst(root);

    while(!stack.isEmpty()){
        root = stack.removeFirst();
        path.add(root.val);
        if(root.right != null){
            stack.addFirst(root.right);
        }
        if(root.left != null){
            stack.addFirst(root.left);
        }
    }
}

后序遍历

处理顺序：左右中

遍历方法：可以发现，处理顺序与先序的顺序是有关系的，只需要将先序的左右颠倒再整体颠倒就是后序的顺序。

中左右 => 中右左 => 左右中

private void PostOrder(TreeNode root){
    Deque<TreeNode> stack = new ArrayDeque<>();
    stack.addFirst(root);
    while (!stack.isEmpty()){
        root = stack.removeFirst();
        path.add(root.val);
        if(root.left != null){
            stack.addFirst(root.left);   //颠倒入栈顺序
        }
        if(root.right != null){
            stack.addFirst(root.right);
        }
    }
    Collections.reverse(path);
}

中序遍历

处理顺序：左中右

遍历方法：因为中序遍历最先处理的节点是左子树上的最左节点，而不是根节点，因此，我们必须首先找到这个节点，利用栈将途径的节点存储下来，便于待会的回溯；找到后，访问该节点，再访问该节点的右子树（或许有人会问，为啥不访问该节点的左子树，呵呵，因为，这个节点已经是最左节点，不会存在左子树），如果没有右子树，那么就会出栈一个元素（也就是刚才那个元素的父亲节点，至于为什么会访问这个父亲节点呢，因为它的左子树已经访问完全啦），继续访问，再访问其右子树，以此类推下去。

private void InOrder(TreeNode root){
    Deque<TreeNode> stack = new ArrayDeque<>();
    while (root != null || !stack.isEmpty()){
        //找到最左子节点
        while(root != null){
            stack.addFirst(root);
            root = root.left;
        }
        root = stack.removeFirst();
        path.add(root.val);
        root = root.right;
    }
}

层次遍历

处理顺序：按层来进行处理

遍历方法：一开始我以为层次遍历是最麻烦的，我甚至在方法的参数中加上了层数的信息，最后发现，呵呵呵，好像不是很难。层次遍历，字面意思，遍历完一层再去遍历下一层。因此，将根节点入队后（这里我用的是队列，其实是Deque的队列属性），再出队一个元素，访问（第一层），再将该节点的左节点，右节点依次入队；出队一个元素，访问（第二层），再将该节点的左右节点依次入队；再出队一个元素，访问（第二层最后一个元素，结束）。以此类推。

其实呢，仔细观察会发现，每次访问完一层后，下一层的所有元素都会被入队（注意，队列是先进先出）。

private void LevelOrder(TreeNode root){
    Deque<TreeNode> stack = new ArrayDeque<>();
    stack.addFirst(root);   //主要是用来记录每一层从左到右的节点
    while (!stack.isEmpty()){
        root = stack.removeLast();   //注意，这里使用的是removeLast而不是removeFirst
        path.add(root.val);
        //将该节点的左节点与右节点放入
        if(root.left != null){
            stack.addFirst(root.left);
        }
        if(root.right != null){
            stack.addFirst(root.right);
        }
    }
}

结束

以上就是我在做这道题的时候，想把二叉树的几种迭代遍历方法都写一遍，加深印象（毕竟一般情况下，都是直接用的递归），为以后的自己留点笔记吧～

番剧啥的，等等吧，最近已经被这疫情堵在寝室里，搞得人有点堵得慌～白白啦！