morris遍历算法

发布: 分类: 评论次数： 阅读次数： 本文字数： 1.9k

博主又开始水文章了，至于为啥我这么积极的写呢？因为在封校期间，博主是很懒的，啥也不想干～昨晚终于将leetcode刷到了第99题！别问我为啥不直接刷到100题，为啥喽？因为我想纪念下刷题数量过百这个大事情～（虽然对各位大佬来说，这都是小case啦，洒洒水啦～）

今天想讲下我在第99题中看到的一种新的算法思路，之前在这类题上还没想过可以这么做。。

题目介绍

1
给你二叉搜索树的根节点root，该树中的恰好两个节点的值被错误地交换。请在不改变其结构的情况下，恢复这棵树 。

1
2
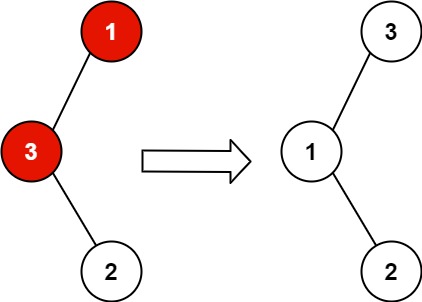
3
输入：root = [1,3,null,null,2]
输出：[3,1,null,null,2]
解释：3 不能是 1 的左孩子，因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。

思路分析

普通思路

其实，这道题，在思路上还是很直接的，因为，我们应该都知道，对于二叉搜索树来说，如果对其进行中序遍历，得到的应该是一个升序的序列，所以，只需要我们对破坏过的BST进行中序遍历，就会发现得到的序列中存在不正确的地方。

但是，需要注意，我们假设不正确的地方被记为x与y（有前后顺序），那么原本的大小关系应该是x < y， 但是得到的序列中为x >= y，这样的地方在序列中可能存在一个或者两个（原因很简单，[1，2，3，4]，如果只是调换相邻的两个数，就是一个，如果调换的不是相邻的就是两个）。

了解这些后，其实大体上，这道题就可以开始做了，我们最初的想法就是把这样的x与y都找到，在将第一个出现的x与最后一个y调换就可以了。至于怎么找到，其实方法也很简单，直接对BST进行中序遍历，并记录当前节点的pre node，访问当前节点的时候，将其与pre node的值比较，如果不正确，就直接记录下当前节点的pre node（x），并且把当前节点记为y，这样的话，x就不用再改变，只需要根据不正确的数量来判断是否需要修改y（其实，也就是在后续的遍历中，如果再次遇到不正确的情况时，只需要更新y，也就是记录最后一个不正确的node）。

这种方法，在时间复杂度上是O(N)，N为节点数量，空间复杂度为O(h)，h为BST的树高（因为中序遍历无论是递归还是迭代都是需要栈空间的）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
TreeNode x, y, pre;

public void recoverTree(TreeNode root) {
  Inorder(root);
  //更换
  int temp = y.val;
  y.val = x.val;
  x.val = temp;
}

private void Inorder(TreeNode root){
  if(root == null){
    return;
  }
  Inorder(root.left);
  if(pre != null && root.val <= pre.val){
    y = root;
    if(x == null){
      x = pre;
    }else{
      return;
    }

  }
  pre = root;
  Inorder(root.right);
}

但是这道题还有一个另外的限制，就是需要将空间复杂度降低为O(1)，常量空间。因此这里就需要引出一个比较厉害的遍历算法，众所周知，对于二叉树的遍历，一般情况下都是需要利用到栈的空间，这也就造成遍历二叉树“不可避免”的空间需求～

但是，存在这么一种方法，它在遍历二叉树的时候，只需要常量级别的空间即可。没错，这就是morris遍历算法，接下来我将使用这种方法介绍如何解决这道题目。

进阶思路

morris算法的关键在于，如何更好的去利用节点的空指针（左右孩子如果为空，则有空闲的指针可以使用），对于遍历二叉树，大家需要有一个观念上的正确，首先，遍历时我们需要使用到每个节点的指针，进而可以找到其孩子节点，这是关键，但是遍历的时候总是存在一个问题，那就是一旦遍历到叶子节点，就会发生回溯的过程，也正是这个过程造成我们需要使用栈的原因。

因此我们可以想，既然一到叶子节点就会回溯，那我们只需要让叶子节点消失不就好了？当然，这里不只是叶子节点，对于中序遍历而言，当我们遍历完左子树后，尤其是左子树的最右节点，我们就需要访问根节点，因此对于所有的有左子树的根节点而言，如果能将访问根节点前一个节点的右指针（一定是空的，不然会继续去遍历该节点的右子树）指向根节点，那么，当左子树访问完全后，便可以直接通过这个新增的指针访问根节点，而不必进行回溯操作。

从上面的一些简单分析来看，相信大家已经能猜到morris算法的一个大概思路是啥。

morris遍历的实现原则：

记当前节点为cur：

  1. 如果cur无左孩子，cur向右移动（cur = cur.right）
  2. 如果cur有左孩子，找到cur左子树上最右的节点，记为MostRight
    1. 如果MostRight的right指针指向空，让其指向cur，cur向左移动（cur = cur.left）
    2. 如果MostRight的right指针指向cur，让其指向空，cur向右移动（cur = cur.right）

举例说明：

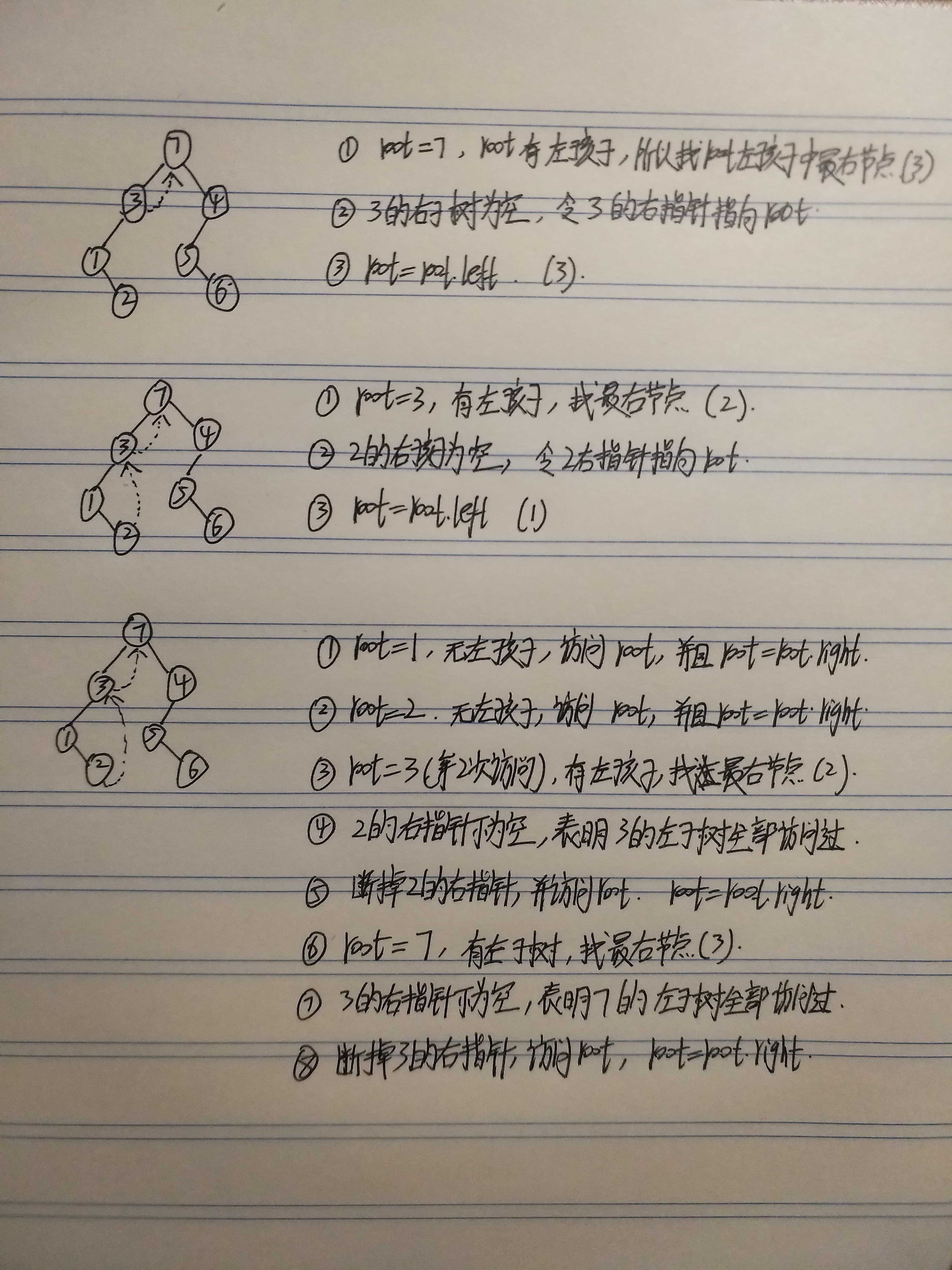
上面这张图呢，是我根据遍历原则对图中二叉树中根节点左子树遍历的一个过程，大家可以好好了解下，当然，对于这道题来说，我们需要解决的是找到有问题的两个节点，其实，寻找方法和第一种常规思路是类似的，还是需要在遍历的过程中对当前节点与pre node进行比较判断。

算法分析：

由于需要找到当前节点的左子树中的最右节点，因此对于二叉树中的每一个节点，我们都需要访问两次，因此时间复杂度为O(2N)，空间复杂度为O(1)。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
public void recoverTree(TreeNode root){
    TreeNode pre = null, x = null, y = null, temp = null;
    while (root != null){
        if(root.left != null){
            temp = root.left;
            //temp.right != root 是用来判断root的左孩子是否遍历完全
            while (temp.right != null && temp.right != root){
                temp = temp.right;
            }
            if(temp.right == null){
                temp.right = root;
                root = root.left;
            }else{
                //表示root的左子树已经访问完全
                if(pre != null && root.val <= pre.val){
                    x = root;
                    if(y == null){
                        y = pre;
                    }
                }
                //断圈
                temp.right = null;
                pre = root;
                root = root.right;
            }
        }else{
            //直接访问右孩子
            if(pre != null && root.val <= pre.val){
                x = root;
                if(y == null){
                    y = pre;
                }
            }
            pre = root;
            root = root.right;
        }
    }
    //交换x,y节点值
    int temp1 = x.val;
    x.val = y.val;
    y.val = temp1;
}

结束

以上就是我这次想要记录的全部啦，虽然算不上什么特别好的叙述，但是呢，足够以后的我能回忆起这个遍历算法。最近在我们学校的社区里竟然还看到了区间极值之类的算法，虽然我也看不懂，但是听起来就很牛逼～

白白啦，下次动漫走起（虽然这几天也没看啥番～）^v^