买股票的那点事

今天是封校的第几天了呢？我也不记得了，不过嘛，现在已经可以每日外出买饭了，还是不错的感觉（指屁股不用一直坐在凳子上的感觉～），今天想记录下的是一道蛮有“意思”的题，没错，就是买股票！！！当然，即使做会这道题也不能保证你的股票会卖的多好，哈哈哈！

买股票1

题目介绍

给定一个数组prices，其中，prices[i]表示第i天股票的价格，只能选择在某一天买入一支股票，并在未来的某一天卖出这支股票，设计一个算法计算出能获得的最大利润（只能交易一次）

示例如下：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

我的思路

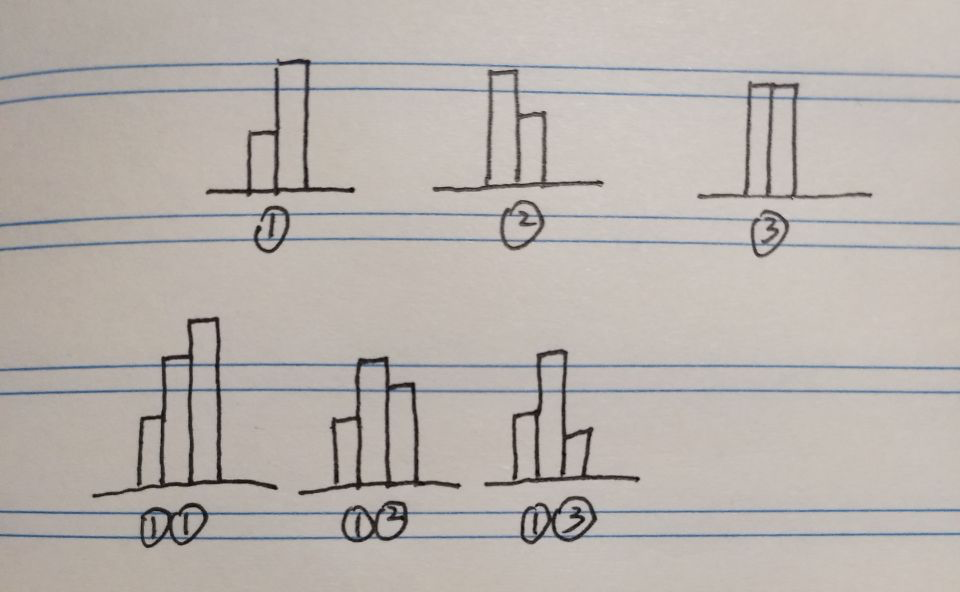
首先我们假设目前正在第i天，并且手上没有股票，既然只能买一次卖一次，那肯定是买的时候价格越低，卖的时候价格越高越好；所以我大致画了上面1，2，3三种情况。

(1) i+1天的价格比i天的价格高，这种时候，我们可以选择i天买入，i+1天卖出，这种情况下一定有的赚，但是是不是赚的最多还不确定。

(2) i+1天的价格比i天的价格低，这种时候，肯定不选择买入，因为即使后面有比i天高的价格存在，那为什么我们不选择在i+1天以更低的价格买入再在那天卖出呢？

(3) i+1天与i天价格相同，这种时候，两天买入都可

注意：这里的买入，不是说是最后的结果中的买入，只是测试型的买入，比如用(1)举例说明，我们并不是说最后的结果中就是i天买入，可能后面还有比i天价格更低的存在，这里只是暂时将目前能得到的最大利润存起来以便后面比较更新。

至于下面三个图，就是针对(1)的扩展，11中i+2天的价格比i天高，所以也需要判断下获得利润是否能变多，12中同样，关键是13中，i+2天的价格比i天的价格还低，那么，我们就会暂时性选择去i+2天买入（目前的最大利润——i+1天卖出，i天买入，已经存好）。

代码

public int maxProfit(int[] prices) {
    int min_price = Integer.MAX_VALUE;  //可以看作第i天的价格（买入的价格）
    int max_index = 0;   //可以看作i+1天及后面的价格指针（卖出的价格指针以及更新买入价格的指针）
    int max = 0;
    int len = prices.length;
    while (max_index < len){
        if(prices[max_index] < min_price){
            min_price = prices[max_index];
        }else{
            max = Math.max(max, prices[max_index] - min_price);
        }
        max_index++;
    }
    return max;
}

买股票2

题目介绍

和买股票1题目大致类似，只是添加了一个条件，可以交易多次，也就是每一天都可以决定买入还是卖出，但是手中最多只能有一支股票（交易次数不限）。

示例如下：

输入: prices = [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

我的思路

其实大致思路和股票1是类似的，只是现在需要明白，只要i+1天的价格比i天价格高的话，我就选择i天买入i+1天卖出，而不会去看i+2天的价格是什么样子的，因为即使i+2天的价格更高，我依旧可以在i+1天买入i+2天卖出；也就是说我会尽可能快的将手中的股票卖出，当然，买入的时候，还是需要价格越低越好（意思就是: i天的价格高于i+1天的价格，但是低于i+2天，那我会选择去i+1天买入，而不是i天）

代码

public int maxProfit(int[] prices) {
    int min_price = Integer.MAX_VALUE;
    int len = prices.length;
    int sum = 0;
    for(int i = 0; i < len; i++){
        if (prices[i] >= min_price) {
            sum += (prices[i] - min_price);
        }
        min_price = prices[i];
    }
    return sum;
}

买股票3

这道题也是这三题中我个人觉得比较难的一道，因为，有点难想～其实呢，在做第一道题的时候，我就已经想到了动态规划这个想法可能能用上，只是因为前两题思路都很直接，就没多想，结果到了这，呵呵，直接懵圈！！！

题目介绍

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。（最多只能交易2次）

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例如下：

输入：prices = [3,3,5,0,0,3,1,4]
输出：6
解释：在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。
     随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3 。

官方思路

思路1

首先，明确这道题的解法是动态规划；其次，动态规划需要有状态转移方程；最后，初始化的条件是什么？我们一样一样来说～

由于这里有三个不定变量（第几天，交易几次，手上有没有股票），所以我们选择定义一个三维的dp数组；其实呢，前两个变量倒好想，就是最后一个手上有没有股票这个不是很好想，为什么非得有这个呢？因为如果手上有股票那就不能再买入，手上没有股票同样也不能卖出。

分析到这，相信很多小伙伴会发现，最关键的地方还没有出现，没错，转移方程！

dp[i][j][k]表示啥意思，上面已经解释过了，这里不作过多解释；其中，j可以选择的值有：0，1，2；k可以选择的值有：0，1.

因此两者可以有6种组合：

• j = 0，k = 0，表示到今天结束为止，我没交易过（指没卖出去过），手上没有持股，所以其利润一定是0
• j = 0，k = 1，表示到今天结束为止，我没交易过，但是手上有一支股票，表明我在今天或者今天之前某一天只买过一支股票，但是没有卖出去，所以其利润有两个选择：今天才买的这支股票（dp[i-1][j][0] - prices[i]）；今天之前就已经买了这支股票，今天没有任何操作而已（dp[i-1][j][1]）。注意：今天之前表示可能是昨天买的，也可能是昨天之前买的，但是不管怎样，利润的积累一定会积累到昨天的dp值上。
• j = 1， k = 0，表示到今天结束为止，我交易过一次，并且手上没有股票，这说明可能到昨天结束的时候我手上还有股票，但是今天我给卖了，还有一种可能就是到昨天结束为止我就已经没有股票在手上了～所以利润也有两选择（dp[i-1][j-1][1] + prices[i]和dp[i-1][j][0]）。
• j = 1，k = 1，这表示到今天结束为止，我交易过一次，并且手上还有一支股票（肯定是第二次买入的，只是买入时间不定），则利润同样有两种可能（dp[i-1][j][1]和dp[i-1][j][0] - prices[i]）。
• j = 2，k = 0，表示到今天结束为止，我交易两次了（到达上限），并且手上没有持股，则有可能我昨天结束时还有股票在手上，只是今天给卖了，同样也有可能昨天结束的时候我手上就没有股票了，所以也有两种可能（dp[i-1][j-1][1] + prices[i]和dp[i-1][j][0]）
• j = 2，k = 1，表示我交易过两次，并且手上还有一支股票（因为这里定义的是卖出为一次交易，所以还是合法的，但是如果事先定义的是买入为一次交易，则这里就是不合法的）手上的这支股票可能是今天购入，也可能是昨天或之前就已经购入，所以利润有两种可能（dp[i-1][j][0] - prices[i]和dp[i-1][j][1]）

整体上看来，其实就分为两种情况

• k = 1时： dp[i][j][k] = max(dp[i-1][j][0] - prices[i]，dp[i-1][j][1])
• k = 0时（因为可能会用到j-1，所以需要分开考虑）：
  • j = 0时，则肯定赚不到钱，利润为0；
  • j != 0时，dp[i][j][0] = max(dp[i-1][j][0]，dp[i-1][j-1][1] + prices[i])

既然，转移方程都写出来了，剩下的就是初始化的问题了，也就是i = 0的情况下，这6种组合的值分别为多少：

• j = 0，k = 0，啥都没干自然是没钱
• j = 0，k = 1，没卖出去过反而还买了一次，自然是亏本（-prices[0]）
• j = 1，k = 0，卖出去过一次，手上没有股票，注意，这是第0天，那肯定是买了第0天的股票立马又卖出去了，所以呢，不亏不赚
• j = 1，k = 1，卖出去过一次，手上还有一支股票（可以理解为第0天的），那就可以理解为买了第0天的股票，又立马卖出去了，然后又立马买回来了（第0天的），所以总体上还是亏本（-prices[0]）
• j = 2，k = 0，卖出去过2次，手上没股票，按照上面的思路，自然是没赚钱没亏钱
• j = 2，k = 1，卖出去过2次，手上还有一支股票（第0天的），亏钱（-prices[0]）

初始情况也分析好了，那代码也就好写了：

public int maxProfit(int[] prices) {
    int len = prices.length;
    int[][][] dp = new int[len][3][2];

    //初始化
    for(int i = 0; i < 3; i++){
        dp[0][i][1] = -prices[0];
    }

    //迭代
    for(int i = 1; i < len; i++){
        for(int j = 0; j < 3; j++){
            //手上有股
            dp[i][j][1] = Math.max(dp[i-1][j][0] - prices[i], dp[i-1][j][1]);
            //手上没有股
            if(j == 0){
                dp[i][j][0] = 0;
            }else{
                dp[i][j][0] = Math.max(dp[i-1][j-1][1] + prices[i], dp[i-1][j][0]);
            }
        }
    }
    return Math.max(Math.max(dp[len-1][0][0], dp[len-1][1][0]), dp[len-1][2][0]);
}

这里简单说明下最后的返回值，因为当最后一天手上还有股票的话，那一定是用之前赚的钱中的一部分去买的（可以这么理解，一开始本金为0，买入就是负的，卖出就是正的，累加起来就是最后的利润，利润是负就是亏钱，利润是正就是赚钱），所以最后一天手上有股票一定是比没股票赚的少，因此我们只需要从最后一天手上没股票的几种情况中找出最大值即可。

思路2

可以发现，思路1中的空间复杂度有点高（n^3），并且呢，上面说的6种组合，其实也可以理解成每天结束时的一个状态，当然肯定是需要重新分组的啦！

状态有以下5种：

1. 到目前为止啥也没做
2. 到目前为止买过一次，但没卖出去过
3. 到目前为止买过一次，卖过一次（表示目前手上肯定没股票）
4. 到目前为止买过两次，卖出去过一次（表示手上目前肯定有股票）
5. 到目前为止买过两次，卖出去两次（手上没有股票）

所以呢，完全可以直接设置dp[i][j]的二维数组，进而优化空间，至于状态转移方程呢，和上面一样分析即可

public int maxProfit(int[] prices){
    //每天结束后只会有5个状态
    int len = prices.length;
    int[][] dp = new int[len][5];
    //初始化
    dp[0][0] = 0;
    dp[0][1] = -prices[0];
    dp[0][2] = 0;
    dp[0][3] = -prices[0];
    dp[0][4] = 0;
    for(int i = 1; i < len; i++){
        dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]);
        dp[i][2] = Math.max(dp[i-1][2], dp[i-1][1] + prices[i]);
        dp[i][3] = Math.max(dp[i-1][3], dp[i-1][2] - prices[i]);
        dp[i][4] = Math.max(dp[i-1][4], dp[i-1][3] + prices[i]);
    }
    return dp[len-1][4];
}

思路3

思路2呢，空间复杂度总觉得还是有点高（n^2），我们发现啊，其实也就4个变量一直在变动，那为什么不直接设置4个变量做呢？

4个变量如下：

1. buy1: 表示到目前为止买过一次，没卖过
2. sell1: 表示到目前为止买过一次，卖过一次
3. buy2: 表示到目前为止买过两次，卖过一次
4. sell2: 表示到目前为止买过两次，卖过两次

这样就完美覆盖了上面的后四个状态，至于为啥第一个状态不用呢，因为啥也不操作自然利润也不会变化

public int maxProfit(int[] prices){
    //使用变量
    //将买入的价格记为正
    int len = prices.length;
    int buy1 = prices[0];
    int sell1 = 0;
    int buy2 = prices[0];
    int sell2 = 0;

    for(int i = 1; i < len; i++){
        buy1 = Math.min(buy1, prices[i]);
        sell1 = Math.max(sell1, prices[i] - buy1);
        buy2 = Math.min(buy2, prices[i] - sell1);
        sell2 = Math.max(sell2, prices[i] - buy2);
    }
    return sell2;
}

注意：我上面的代码中，buy1和buy2表示的是买入价格（比如buy2，prices[i] - sell1是指买了i天的股票，用的钱呢在sell1中扣，sell1自然是卖过一次后手中的钱），所以需要注意是用max还是min，其实很好理解，买入自然越低价格越好，卖出自然价格越高越好。

结束

到这里就结束了，虽然听说好像还有个买股票4，但是我还没做到那，等做到了再说吧，今天（2022-03-25）没错，昨晚太晚了，就没写完，上午又去做了次核酸，还不知道啥时候才可以完全解封～

番剧的话，还在追，劳烦各位lsp等等啦！^V^