今天天气如此之好,怎么能不来刷道leetcode的题呢?额,,解数独???什么鬼,虽然第一眼望去,肯定是回溯没错啦,可是我不会用回溯啊,虽然在此之前已经做过好几道回溯的题,可一旦自己写起来还是不太会。。
![]()
题目介绍
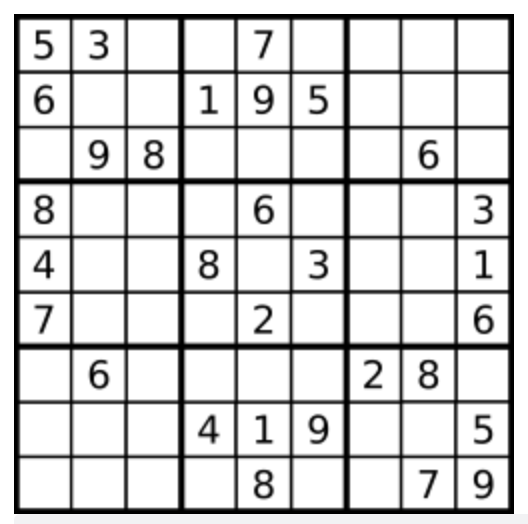
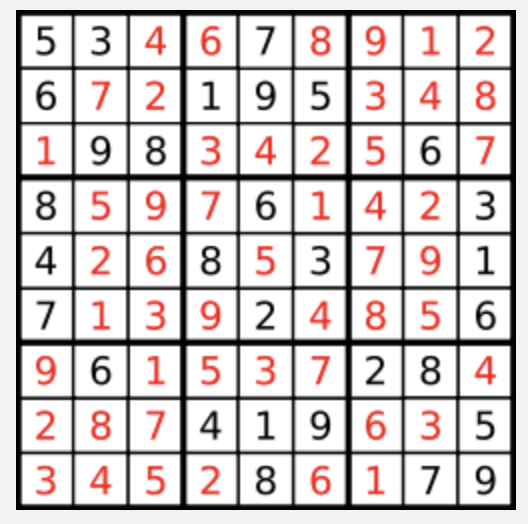
给定一个待解的数独,求解
举例:
![]()
![]()
回溯算法<重点>
所谓的回溯算法,实际上就是常说的DFS算法,深度优先搜索算法等等,再实际点就是递归中的一种,对决策树的一种遍历。
回溯的重点:
- 选择的路径(就是你已经选择完,加入结果的路径)
- 选择的列表(就是目前当下你还可以选择的有哪些)
- 结束的条件(当到达决策树的底层的时候,不再选择的条件)
代码模版:
1
2
3
4
5
6
7
8
9
10
| result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
|
注意:这里backtrack里的参数不是一定非得这样
重要的部分在于for循环内部,首先是做出选择,然后可能会修改路径,修改选择列表等等,再进行递归,最后撤销回溯
解题思路
这道题,咋一看,可能有点难,实际上,仔细一想,针对每一个待填的空格,无非就只有1-9 9种选择,依次往里试填,找到合适的(假设为k),就往下一个待填空格走
因此,执行步骤如下:
- 遍历行列,确定待填空格A的行列后,依次将1-9试填,找到合适的往下走
- A填完后,下一个空格假设为B,同样,依次1-9试填,找到后,继续往下;如果1-9都不行,那么表示A或者A与A之前的空格都填错了,因此就需要回溯,简单点说,就是往回走,修改前面填过的。修改过程看下一步
- 针对当前空格无法填入的问题,回溯修改,首先回溯到A空格,将A中填入的数字k用’.’代替,重新到步骤1中,从k到9继续试填,找到了往下走,如果k-9也没有合适的,表示A之前的空格填错了,继续类推往前修改
由于这里只需要找到一种解法就可以,因此回溯模版中的返回类型可以用boolean代替
模版可以填充为下面这种形式:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| def backtrack(棋盘):
因为只要棋盘填满就可以返回,所以这里可以不设置返回条件
for 每个待填的空格 in 棋盘:
for 选择 in 选择列表(1-9):
if(选择填入后合适):
填入(做选择)
//由于只需要一种解法,因此找到一组能填满棋盘的路径就返回
if(backtrack(棋盘)): return true
//后面某个空格没数字合适填入,就修改当前的空格数字
撤销选择
//没有一个合适的数字能填入,返回false
return false
//待填的都填完了,返回true
return true
|
具体代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| public void solveSudoku(char[][] board) {
backtrack(board);
}
private boolean backtrack(char[][] board){
for(int i=0;i<board.length;i++){
for(int j=0;j<board[0].length;j++){
if(board[i][j]!='.'){
continue;
}else{
for(char k='1';k <= '9'; k++){
if(isValid(board,i,j,k)){
board[i][j] = k;
if(backtrack(board)){
return true;
}
board[i][j] = '.';
}
}
return false;
}
}
}
return true;
}
private boolean isValid(char[][] board, int row, int col, char target){
for(int i=0;i<board[0].length;i++){
if(board[row][i] == target){
return false;
}
}
for(int i=0;i<board.length;i++){
if(board[i][col] == target){
return false;
}
}
int s1 = (row/3)*3;
int s2 = (col/3)*3;
for(int i=s1;i<(s1+3);i++){
for(int j=s2;j<(s2+3);j++){
if(board[i][j]==target){
return false;
}
}
}
return true;
}
|
结束
leetcode后面还会有不少回溯类型的题目,希望到时候自己能一次做出来啊
番剧啥的,等!!这周六周末一定写!!