kd树与KNN方面的小小认识

发布: 分类: 评论次数： 阅读次数： 本文字数： 2.6k

今天呢，有点小特殊，为什么这么说呢，因为这是我第一次在寝室里写这种博文。或许有人会问，为什么这就算特殊呢？哈哈哈，因为博主是一个好动的人，几乎不咋呆寝室，这次是因为紧急情况（宿舍楼被封了，，疫情真讨厌～）

这次想说的是我正在读的一本书（统计学习方法）中的一个小点—kd树在knn中的应用。其实呢，这在机器学习这个领域内算是入门级别的知识，我就单纯记点我的想法（望大佬勿喷）

kd树的介绍

首先，kd树可以理解成是一种二叉树，只不过这种二叉树比较特殊而已，至于特殊在哪，还请往下看～

给出一组数据，可以更好地解释kd树的构成，数据如下：

1
T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}

这是一个二维的数据，现在我将使用这些数据演示下kd树的构建过程，这样的话，我觉得可能会更容易理解，在往下看之前，我就先默认大家都清楚平衡二叉树的概念啦

构建kd树一定要注意维度的概念，就拿T数据举例来说，这个数据中包含了dim = 0与dim = 1（因为是二维的嘛）

构建过程：

  • dim = 0: 将T中的数据按照第0维的数字先排个序，排完序之后为：T = {(2,3),(4,7),(5,4),(7,2),(8,1),(9,6)}，接下来呢，取中位数（7，2）作为kd树的根节点，注意：这里是向下取整，中位数左边的呢，作为根节点的左子树节点，右边的自然就是右子树啦
  • 先看左子树，T_left = {(2,3),(4,7),(5,4)}，按照同样的原理，只不过这次看的不是第0维，而是第1维，将T_left按照第1维数字的大小进行排序，即T_left = {(2,3),(5,4),(4,7)}，取中位数（4，7）作为左子树的根节点，其左右分别作为该节点的左右子树
  • 继续看左子树，T_left’ = {(2,3)}，这时看的维度又需要变回第0维，相信聪明的小伙伴，已经看出，维度的变化在于树的深度与给定数据的维度之间的某种关系：深度 % 维度
  • 右子树的构建也是如此，只是需要注意，树每一层看的维度都是一样的

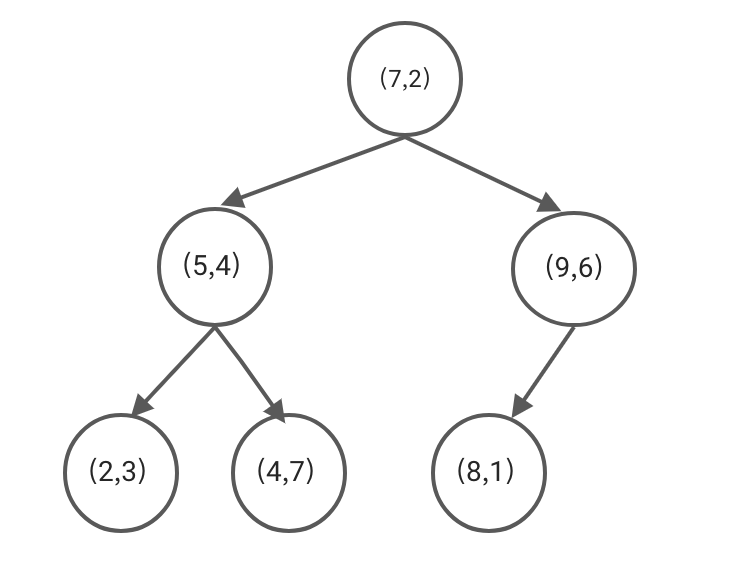
也许细心的同学已经发现，在建树的过程中，维度依据的变化是不是并不太合理呢？确实是这样的，因为如果只是按照顺序来选择特征维度（可以把每个维度理解成一种特征类型或者特征标签），是不是并不能保证划分数据或者实例点很简单呢？因此，后面有人想出了一个方法，既然想要更容易区分，那这不正好符合方差的定义嘛，没错，在每一次选择节点的时候，依据维度的选择不再是简单的按照顺序来判断，而是先判断下当前数据集中哪一个维度的数字方差更大，越大表示越容易区分.

KNN算法的简单介绍

KNN算法，全称为k近邻算法，它主要是用来做分类预测的，所依据的无非是多数决策的手段，简单点来说，就是指判断一个数据点的时候，先找到它的k个最近的邻居，看看这k个邻居中哪种类别占多数，那这个数据点就会被划分到那一类。

既然要找k个最近的邻居，就要牵扯到距离的定义，一般情况下，我们常用的就是欧式距离等等，具体有哪些距离，可以看看下面
$$
L_p(x_i,x_j) = (\sum_{l=1}^n |x_i^{(l)} - x_j^{(l)}|^p)^{\frac{1}{p}}
$$
（1）p = 2时，该距离便是欧式距离

（2）p = 1时，该距离为曼哈顿距离

（3）p = 无穷时，该距离为切比雪夫距离
$$
L_p(x_i,x_j) = max_i(|x_i - x_j|)
$$
怎么说呢，老实说，KNN算法在理解上是很简单的，只是它需要快速地找到与target最近的邻居，因此如果只是单纯地去寻找是不可接受的（复杂度过高），这时就需要使用kd树出场啦，怎么使用呢，我们依旧以上面的那棵kd树来举例说明

1
2
3
target = (2, 4.5)

kd tree: 上图

第一步，和平衡二叉树是很类似的去查找，只不过这里需要将维度也考虑进去，比如说，从树的根节点开始，由于这一层的维度是0，所以将target[0]与根节点的第0维数据比较，大于则去右子树查找，反之，左子树查找

第二步，找到叶节点(4, 7)，此时将该节点看成是最近点，计算其与目标值的距离，依次回溯之前的查找路径，也就是(5, 4)，判断其与target的距离是否小于最短距离，如果是，则将该点重新看成最近点，再检查该节点（叶节点的父节点）的另外一个子节点，如果该节点在以target为圆心，最短距离为半径的圆内，那么表示该子节点离target更近，因此需要递归地去查找这个子树（和之前一样，直到找到叶节点），如果不在，就直接去判断父节点的父节点（依次回溯），注意：无论父节点是否比当前最近点离target近，都需要去判断父节点的另一子节点是否在圆内

第三步，直到回溯到根节点，当前的最近点就是target的最近邻

比较关键的地方在于，需要判断当前节点的父节点的另一子节点是否需要去search，这里涉及到递归的含义。当然，这里只是找到一个最近邻而已，我们需要找到k个近邻，因此至少需要查找k次，每一次的复杂度在log(n)，k次就是klog(n)，n为节点的个数

构建kd树的实现

先上代码吧，有点小傻，别笑，我写完后，看了下网上的思路，都要么是利用了方差，要么就是想的比我简洁点，待会说下简洁的地方在哪

1
2
3
4
5
6
7
class Node(object):
    # 节点类
    def __init__(self, val=-1, dim=0, lchild=None, rchild=None):
        self.val = val
        self.dim = dim
        self.lchild = lchild
        self.rchild = rchild
1
2
3
4
5
6
7
8
9
10
11
12
13
# 建树
def create_tree(self, nodes, i, left, right):
    if left >= right:
        return None
    if i == len(nodes[0]):
        i = 0
    nodes_temp = sorted(nodes[left:right], key=lambda x: x[i])
    nodes[left:right] = nodes_temp
    index = int((right + left) / 2)
    root = Node(nodes[index], i)
    root.lchild = self.create_tree(nodes, i + 1, left, index)
    root.rchild = self.create_tree(nodes, i + 1, index + 1, right)
    return root

其实呢，这也可以看成是一个简单的构建二叉树的过程，只不过是需要加上数据的选择罢了，以往的构建二叉树，只需要将给定的数据按照二叉树的结构放进去就可以，现在需要考虑到数据之间的“大小关系”，可以看到，代码中的参数包括了left与right，这就是为了判断当前需要判断数据的列表是从哪里到哪里使用的，以及为了计算中位数的下标使用的（后面的是主要），结果看了网上的代码，我彻底呆了～

为啥呢，因为python中如果只想用某个数组的一部分，可以直接这样：nodes[:medium_index]之类的，至于求中位数嘛，我傻了，可以直接用len(nodes) / 2来获取，哈哈哈哈～

KNN最近邻算法实现

老样子，先上代码，不一定对，感觉像是对的（虽然没啥信心）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
def get_dis(self, a, b):
    if len(a) != len(b):
        return -1
    # 采用欧式距离
    dis = 0
    for i in range(len(a)):
        dis += (a[i] - b[i]) * (a[i] - b[i])

    return math.sqrt(dis)

# 最近邻
def search(self, target, root, path):
    global visited
    global nearest_point
    global min_dis
    # 顺序查找直到叶节点
    while root is not None:
        path.append(root)
        if target[root.dim] < root.val[root.dim]:
            root = root.lchild
        else:
            root = root.rchild
    # 回溯
    while len(path) != 0:
        point = path.pop()
        dis = self.get_dis(point.val, target)
        visited.append(point)
        if dis < min_dis:
            nearest_point = point
            min_dis = dis
        # 回退到根节点，直接返回
        if len(path) == 0:
            break
        if point.lchild is not None and self.get_dis(target, point.lchild.val) < min_dis and point.lchild not in visited:
            self.search(target, point.lchild, path)
        if point.rchild is not None and self.get_dis(target, point.rchild.val) < min_dis and point.rchild not in visited:
            self.search(target, point.rchild, path)
    return nearest_point.val

也没什么好说的，原理就摆在那，除了我不太会搞递归，是真的不太会，脑子总是转不过来（^V^)

结束

就这样啦，《统计学习方法》这本书还是挺不错的，推荐大家去看看，挺适合没啥基础的同学去看看，哦，对了，下部番快好啦，很快就可以推给大家啦！！！好好期待吧～