今天又是周日,每周最开心的一天,因为今天可以感受到那种难以忘怀的刺激感。每周日的上午,我习惯性地打一场leetcode的比赛,因为只有比赛时才让我有种在用脑子的感觉。虽然我现在还是个菜鸟,但是还是有那么一点点的提升的~
今天的比赛,怎么说呢,自己做的不是很好,甚至可以说是最近打的最差的一次了(虽然A了三题,但是依旧掉大分),总体上来说,只有T4挺难的,T3想复杂了,一个贪心就行了,我还非得用dfs来几次TLE。下次继续努力~
![]()
今天主要是想记两道题目,一道是今天周赛,也就是339的T4,一道是昨晚夜周赛101的T4,两道题用的核心思路都是BFS(是不是很巧~)
339的T4
题目介绍
给定一个数组arr,长度为n,下标从0开始,给定一个p(p在0到n-1之间),表示数组arr中除了p位置为1以外,其他都是0;给定一个banned数组,arr中下标在banned中的所有数不能为1;给定k,表示每次操作可以将一个长度为k的子数组翻转(指顺序上的翻转);返回一个数组答案ans,其中ans[i]表示将1移动到i位置所需要的最少操作次数,无法翻转到的设置为-1.
注意:任何操作都不允许将1翻转到banned中的下标位置(原题)
1
2
3
4
5
| 输入:n = 4, p = 0, banned = [1,2], k = 4
输出:[0,-1,-1,1]
解释:k = 4,所以只有一种可行的翻转操作,就是将整个数组翻转。一开始 1 在位置 0 处,所以将它翻转到位置 0 处需要的操作数为 0 。
我们不能将 1 翻转到 banned 中的位置,所以位置 1 和 2 处的答案都是 -1 。
通过一次翻转操作,可以将 1 放到位置 3 处,所以位置 3 的答案是 1 。
|
1
2
3
4
5
| 输入:n = 5, p = 0, banned = [2,4], k = 3
输出:[0,-1,-1,-1,-1]
解释:这个例子中 1 一开始在位置 0 处,所以此下标的答案为 0 。
翻转的子数组长度为 k = 3 ,1 此时在位置 0 处,所以我们可以翻转子数组 [0, 2],但翻转后的下标 2 在 banned 中,所以不能执行此操作。
由于 1 没法离开位置 0 ,所以其他位置的答案都是 -1 。
|
我的思路
没有(///▽///),比赛时没做出来,还是菜
官方思路
利用BFS,首先我们需要知道,位置i经过一次翻转,可以到哪些位置去(核心),由于存在一个k窗口,因此可以假设窗口的左端点为t,那么很容易知道i在这样的窗口下,翻转后的位置为:==2t + k - 1 - i==
1
2
3
4
| 根据对称原理:
t + t + k - 1 = i + x
因此:
x = 2t + k - 1 - i
|
那t是否存在范围呢,当然有,如果是无限大的数组,t最小为i - k + 1,t最大为i,但数组有范围,所以t的范围为[left, right]:
1
2
| left = Math.max(0, i - k + 1);
right = Math.min(n - k, i);
|
从翻转后i所在的位置表达式中可以看出,窗口每向右移动一个,翻转后的位置就移动2个,因此翻转后的位置奇偶性是保持一致的,是奇数还是偶数取决于k - 1和i的关系。
因此,为了避免重复性将跳到过的位置加入队列,可以将0到n-1这些数,除了p和banned里的数以外,按照奇偶性放入两个TreeSet中,这样就可以实现翻转到过的下标就立马删除,并且可以在O(logn)的时间里找到第一个翻转的下标(利用TreeSet的ceiling(x)方法,表示找到第一个大于等于x的数,没有的话返回null)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| class Solution {
public int[] minReverseOperations(int n, int p, int[] banned, int k) {
int[] ans = new int[n];
Arrays.fill(ans, -1);
if(k == 1){
ans[p] = 0;
return ans;
}
Set<Integer> set = new HashSet<>();
for(int x : banned){
set.add(x);
}
TreeSet<Integer> odd = new TreeSet<>();
TreeSet<Integer> even = new TreeSet<>();
for(int i = 0; i < n; i++){
if(i != p && !set.contains(i)){
if(i % 2 == 0){
even.add(i);
}else{
odd.add(i);
}
}
}
Deque<Integer> queue = new ArrayDeque<>();
queue.addLast(p);
int step = 0;
while (!queue.isEmpty()){
int size = queue.size();
for(int i = 0; i < size; i++){
int root = queue.removeFirst();
if(ans[root] == -1){
ans[root] = step;
}
int left = Math.max(0, root - k + 1);
int right = Math.min(n - k, root);
if(root % 2 == k % 2){
Integer start;
while ((start = odd.ceiling(2 * left + k - 1 - root)) != null && start <= 2 * right + k - 1 - root){
queue.addLast(start);
odd.remove(start);
}
}else{
Integer start;
while ((start = even.ceiling(2 * left + k - 1 - root)) != null && start <= 2 * right + k - 1 - root){
queue.addLast(start);
even.remove(start);
}
}
}
step++;
}
return ans;
}
}
|
其实,如果不用TreeSet的话,暴力解的话,就需要加个辅助数组,用来记哪些位置是已经翻转到过的,避免重复入队,并且在判断从i翻转一次的下标时,需要枚举左端点从left到right,并在该左端点时判断对应的翻转位置是否已经翻到过,这样的话就是O(n^2)的,会超时。
收获
其实,打比赛做到这道题的时候,还剩下半小时(别骂, 因为我太蠢了,在第一题花了蛮长时间~脑子生锈了,第三题想偏了),然后也没有啥思路,就直接原地坐牢到结束。
在数组上利用BFS实现跳跃,感觉这种用法我倒没咋用过,虽然不保证以后遇到变形题会做,但至少知道有这类题了,也算是不错的收获了。
101的T4
这场比赛我没打,因为昨晚有预感,打了得掉大分(即使不打,今天照样掉大分~)
题目介绍(经典题目)
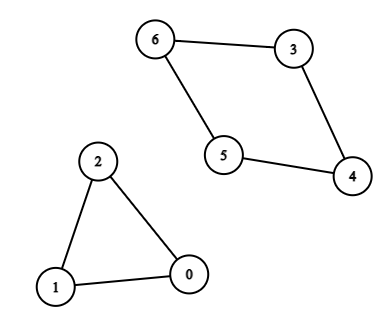
给定一个无向图,边用二维数组edges给出,没有自环、重复边,问最小环的长度
![]()
1
2
3
| 输入:n = 7, edges = [[0,1],[1,2],[2,0],[3,4],[4,5],[5,6],[6,3]]
输出:3
解释:长度最小的循环是:0 -> 1 -> 2 -> 0
|
我的思路
一开始想用dfs去做,结果发现,有点做不出来(///▽///),然后就想BFS,直接枚举BFS的起点,然后得到包含起点的最小环的长度
官方思路
思路1
利用枚举起点+BFS,当针对于出队的点cur与它的父节点fa,我们看cur的邻居节点x,如果发现邻居节点x不是fa但已经访问过或者说入队过,这说明从起点到该邻居节点x有两条不同的路径,也就是形成环了,环的长度为dis[cur] + dis[x] + 1,这时可以选择直接返回,因为是BFS,所以包含起点的最小环不可能比当前的还要小。
注意:这里说的形成环,并不能保证起点到x是一个环,但能保证x一定是环的一个点,比如说有两条路径:1-2-3-5和1-2-4-5,这里1-5就没有形成环,但是无所谓,因为是枚举起点,当起点为2时就可以缩小答案了
由于这里需要记录起点到其他点的距离,因此直接利用dis来标示节点是否被访问过或者说入队过。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| class Solution {
int ans = Integer.MAX_VALUE;
int n = 0;
Map<Integer, List<Integer>> map = new HashMap<>();
private int bfs(int start){
int[] dis = new int[n];
Arrays.fill(dis, -1);
Deque<int[]> queue = new ArrayDeque<>();
queue.addLast(new int[]{start, -1});
dis[start] = 0;
while(!queue.isEmpty()){
int size = queue.size();
for(int i = 0; i < size; i++){
int[] root = queue.removeFirst();
int cur = root[0], fa = root[1];
for(int x : map.get(cur)){
if(x == fa){
continue;
}
if(dis[x] != -1){
return dis[x] + dis[cur] + 1;
}else{
dis[x] = dis[cur] + 1;
queue.addLast(new int[]{x, cur});
}
}
}
}
return Integer.MAX_VALUE;
}
}
|
思路2
利用删除边+BFS,假设原始图里有边i-j,那么我们如果把这条边删掉,再利用BFS(因为边权为1,所以可以直接简单BFS)求i到j的最短路径,如果有最短路径,说明i-j是某个环里的一条边,环长度为最短路径 + 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| class Solution {
Map<Integer, List<Integer>> map = new HashMap<>();
boolean[] visited;
private int bfs(int start, int end){
Arrays.fill(visited, false);
Deque<Integer> queue = new ArrayDeque<>();
queue.addLast(start);
visited[start] = true;
int step = 0;
while(!queue.isEmpty()){
int size = queue.size();
for(int i = 0; i < size; i++){
int cur = queue.removeFirst();
if(cur == end){
return step;
}
for(int x : map.get(cur)){
if(cur == start && x == end){
continue;
}
if(!visited[x]){
queue.addLast(x);
visited[x] = true;
}
}
}
step++;
}
return Integer.MAX_VALUE - 1;
}
}
|
收获
这道题感觉还不错,考的东西比较基础但很实用,BFS的用法在这道题里主要是用来求起点到其他点的最短路径。
整体收获
BFS还是蛮有用的,可以用到的地方很多,还有很多不同的变种。虽然这次周赛掉大分,但是还是收获了不少。