组合总和—回溯和剪枝

发布: 分类: 评论次数： 阅读次数： 本文字数： 1.3k

今天刷的这道题其实上是不难的，只是想拿出来说明一下其中可以在以后做题中运用的地方，也就是这道题的闪光点

至于为啥今天博主太阳从西边起来，竟然刷起了题（别问，问就是在图书馆看了半个小时的番，心里有愧～）

题目介绍

今天我做的题意外的竟然和上次的解数独是一种方法，没错，就是回溯（偷偷瞅了一眼，下一题好像还是回溯）

回溯这种方法说到底还是一种暴力解题的思路（只是名字好听了点罢了，还有就是用了树的思路）

  1. 题目内容：

    给定一个无重复元素的正整数数组 candidates 和一个正整数 target ，找出 candidates 中所有可以使数字和为目标数 target 的唯一组合。

    candidates 中的数字可以无限制重复被选取。如果至少一个所选数字数量不同，则两种组合是唯一的。

    对于给定的输入，保证和为 target 的唯一组合数少于 150 个。

  2. 举例说明：

    1
    2
    输入: candidates = [2,3,6,7], target = 7
    输出: [[7],[2,2,3]]
    1
    2
    输入: candidates = [2,3,5], target = 8
    输出: [[2,2,2,2],[2,3,3],[3,5]]
    1
    2
    输入: candidates = [2], target = 1
    输出: []

思路

这道题一眼看过去，首先应该得画出这张图出来（以上面的第二个例子来讲）：

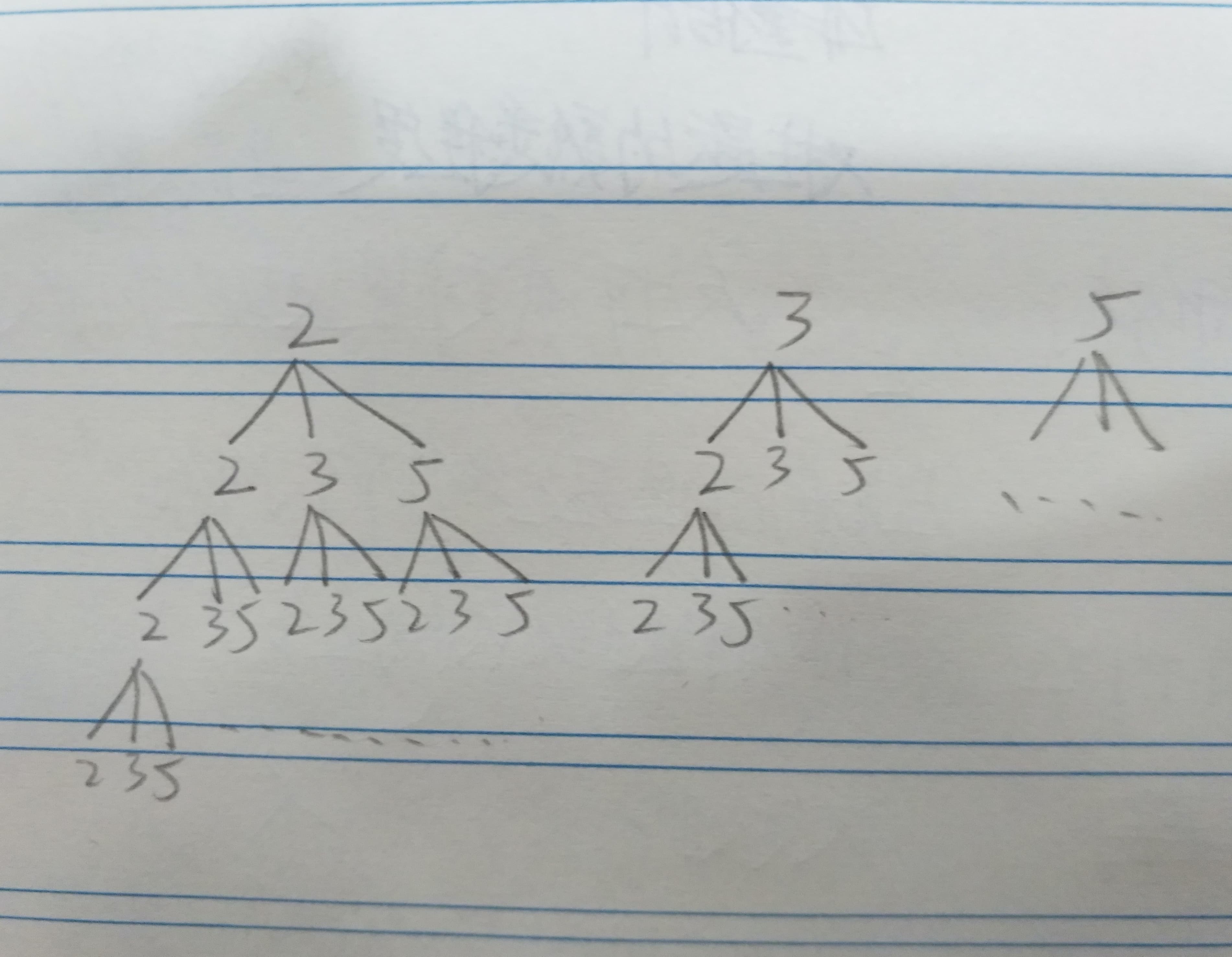
也就是一棵多叉树的结构，因为需要找到所有合适的组合，并且选择列表是不会变化的（这句话在后面的剪枝中会被改变），所以利用这棵树就可以找到所有合适的组合

当然，肯定会有人问，那这棵树不就会无限向下延伸的嘛？话虽是这么说没错，不过可以利用剪枝啊，首先往下剪枝，只要当前路径上的sum大于target，就不往下走了不就好了；既然前面是往下剪枝，那肯定有其他剪枝啦，没错，可以想想看，同一层上，如果我们把选择列表从小到大排个序，比如说，还是以上图举例，我们当前路径上是2，3，3，sum是8也就等于target，那就可以将该路径放入结果中，再回溯，将末尾的3删掉，加入下一个选择5，想想看，这步操作有必要吗，我们前面的3刚好加上去是target，那么比3大的5加上去肯定比target大，所以可以直接将3删掉后，break掉，返回再将末尾的3（倒数第二个）删掉，路径变为2，也就是放回到了图中的第一棵树的根节点处，计算2下面的5分支

再想一个问题（该题的精髓之一），我们第一棵树下会找到一个路径2，3，3，进入第二棵树后，会找到3，2，3；3，3，2，这就重复了，因此得想办法去重，一开始我的思路很直接：要么Hashset，要么排序判断结果中有没有该路径。结果，AC是AC了，只是复杂度太高了（过多的排序）

仔细分析上图，重复的原因是在哪里，很容易看出来，因为在第二棵树中，我们以3开头，往下找，只要路径中出现了2，就可能会重复，为什么呢，因为路径包含2且符合条件的在第一棵树中都已经找出来了,所以可以设计在后面的树中找寻时，直接跳过前面找过的树的根节点，比如说，第二棵树，我们将选择列表中的2直接去掉即可，第三棵树直接将2，3去掉即可

代码

具体的代码，其中的去重部分在回溯函数中的begin控制上，表示回溯到路径为空时，下一步在选择列表中选择的第一个数的下标

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
public List<List<Integer>> combinationSum(int[] candidates, int target) {
    List<Integer> ans = new ArrayList<>();
    List<List<Integer>> ret = new ArrayList<>();

    //排序
    Arrays.sort(candidates);

    backtrack(candidates,target,0,ans,ret,0);

    return ret;
}

private void backtrack(int[] candidates, int target, int sum, List<Integer> ans, List<List<Integer>> ret, int begin){
    if(sum == target){
        List<Integer> temp = new ArrayList<>(ans);
        ret.add(temp);
        return;
    }
    if(sum > target){
        return;   //适当剪枝
    }
    for(int i=begin;i<candidates.length;i++){
        //选择
        ans.add(candidates[i]);
        sum += candidates[i];
        //递归
        backtrack(candidates,target,sum,ans,ret,i);

        if(sum >= target){
            //后面的不用尝试了
            ans.remove(ans.size()-1);
            sum -= candidates[i];
            break;
        }
        //撤销
        ans.remove(ans.size()-1);
        sum -= candidates[i];
    }
    return;
}

结束

以上就是博主做这道题的一些小想法啦，希望能帮助一些和我以前一样对回溯总是想不懂的同学啦，至于开头说的在图书馆里看的那部番呢，不是我主追的那部，图书馆这部呢，是我之前看断掉的一部番（因为各种不可抗力原因啦），也很有趣的，叫做《带着智能手机闯荡异世界》

有兴趣的小伙伴也可以去看看（很有意思的～）