区间问题

发布: 2021-12-04 分类: 学习评论次数：阅读次数：本文字数： 2.7k

又是美好的周六，今天的上海天气是真的好，刚好老爸来学校玩了半天不到，我也趁着这个机会在学校里瞎逛了会。学校里呢，这几天也在办一些活动，比如像冬季长跑啦，以前玩的那种脚并着走路啦，巴拉巴拉的许多。

但该干活的时候，还是得干活的，毕竟我可是留了不少ddl在赶的男人～像啥计算机网络的第二次作业啦，最优化的第十二周作业啦，最优的的论文啦，项目进展啦，学术英语第一次作业啦，等等等等，一大堆。。。。不过嘛，在下午的连忙赶工中，目前只剩下几样啦，可以明天或者有空再慢慢搞了，又恢复到了可以写写流水账的时候啦。

今天想把关于区间类的问题做个小小的总结，因为这类问题其实想起来还是很容易出各种变化的题型的～

今天主要想讲两种类型的区间问题：

区间合并
区间插入

至于区间重叠判断，，应该是最简单的了吧～就不用多讲了

在讲这两种问题前，我先简单介绍下这几天，，也不对，是最近学到的一种结构类型吧，名字叫做“bitset”

关于bitset的解释，我还是选择使用示例来讲，看下面这幅图就大概懂这个类型的用法了：

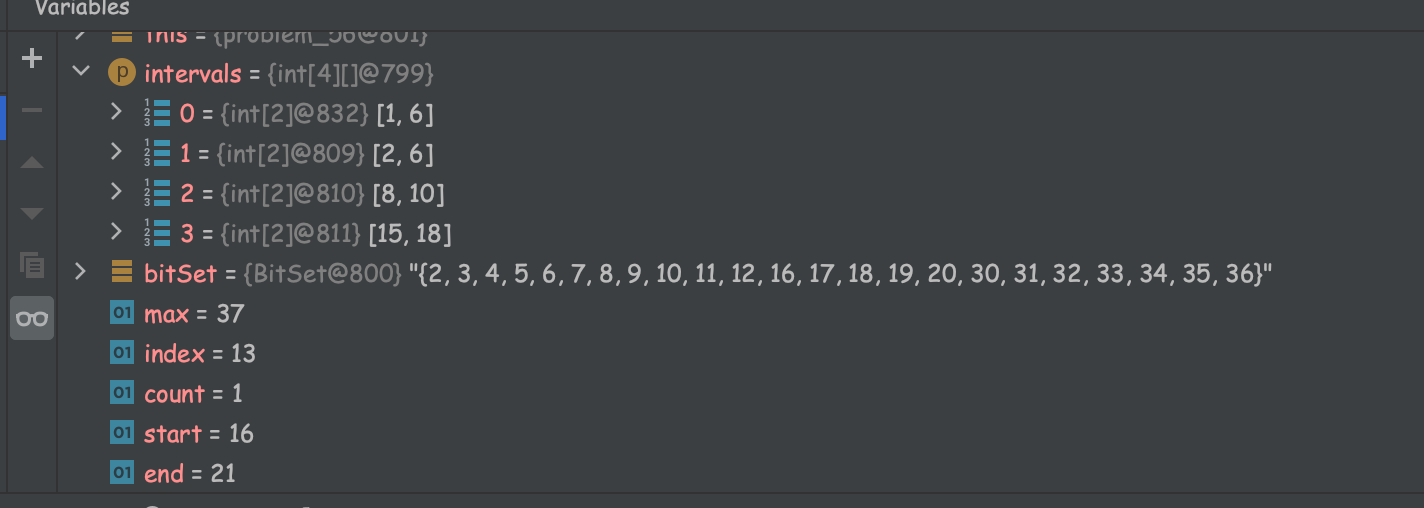
这幅图是我在代码中用到的，首先解释下里面的这些2，3，等值代表什么意思，这些值其实是你原本数组或者其他结构里面的索引，存到bitset里，并且这些值的位置都是被赋予了true。如果还是不太懂，更简单点，就是说2,3,4,5……..36这些值对应的都是true，其他的都是false

关于bitset有三个方法比较常用，一个是nextSetBit()，一个是nextClearBit()，一个是set方法，举例说明这三方法的含义：

nextSetBit(13)：返回的是16，因为16是比13大，并且设置为true的（这里可以包括13）

nextClearBit(16)：返回的是21，因为21比16大，并且设置为false（同样可以包括16）

bitSet.set(0, 3, true): 会在bitset里加入0,1,2

说到这里，想必大家也明白我为什么要先讲这个结构了吧～没错，这个类型在区间问题上是很方便的，因为完全可以把这个bitset看成是坐标轴来使用。

好了，正式开始两种区间问题的简单介绍～

问题类型1: 区间合并

问题介绍

以数组intervals表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间。

1
2
3

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

1
2
3

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。

问题思路

首先，我们需要做什么，给出一个结果集，用来装区间段，然后就是依次遍历题目给定的多个区间，当然，首先得确保这些区间都是按照区间左端点由低到高的顺序排列的，至于为什么，待会就知道了，具体步骤如下：

当结果集是空 or 目前遍历到的区间的左端点大于结果集最后一个区间的右端点时，直接将该区间加入结果集
当遇到目前区间的左端点小于等于结果集最后一个区间的右端点时，表示两者重叠（为啥？画个图你就知道了，这里也就是为啥必须得先排好序才行的原因），既然重叠，那必然是需要合并的啦，至于咋合并，用脚趾头想都能想出来吧，肯定是把结果集中最后一个区间的右端点改下不就好啦，改成啥呢，那得看结果集最后一个区间的右端点与当前区间的右端点谁大了，谁大换谁

上图中的蓝色代表当前区间，黑色表示结果集最后一个区间，从图中就可以看出为什么要在确定合并后区间的右端点时比较大小的原因了。

代码

public int[][] merge(int[][] intervals) {
    // 先按照区间起始位置排序
    Arrays.sort(intervals, (v1, v2) -> v1[0] - v2[0]);
    // 遍历区间
    int[][] res = new int[intervals.length][2];
    int idx = -1;
    for (int[] interval: intervals) {
        // 如果结果数组是空的，或者当前区间的起始位置 > 结果数组中最后区间的终止位置，说明不重叠。
        // 则不合并，直接将当前区间加入结果数组。
        if (idx == -1 || interval[0] > res[idx][1]) {
            res[++idx] = interval;
        } else {
            // 反之说明重叠，则将当前区间合并至结果数组的最后区间
            res[idx][1] = Math.max(res[idx][1], interval[1]);
        }
    }
    return Arrays.copyOf(res, idx + 1);
}

注意：由于一开始并不知道合并后有多少个区间，因此至少需要原本区间的数量大小，返回时可以直接使用copyOf方法拷贝我们创建的数组中的一部分

问题类型2: 区间插入

问题介绍

给你一个 无重叠的 ，按照区间起始端点排序的区间列表。

在列表中插入一个新的区间，你需要确保列表中的区间仍然有序且不重叠（如果有必要的话，可以合并区间）。

1 2	输入：intervals = [[1,3],[6,9]], newInterval = [2,5] 输出：[[1,5],[6,9]]

1
2
3

输入：intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
输出：[[1,2],[3,10],[12,16]]
解释：这是因为新的区间 [4,8] 与 [3,5],[6,7],[8,10] 重叠。

问题思路

从题目上来看，其实这道题相比于前一道题还要简单点，为什么呢，因为题目中给出了区间列表是排好序的，我们只需要将给的新区间放到结果集中，整个过程可以分为三步：

当目前区间的右端点小于新区间的左端点时，直接放入结果集，直到目前区间的右端点大于等于新区间左端点为止。
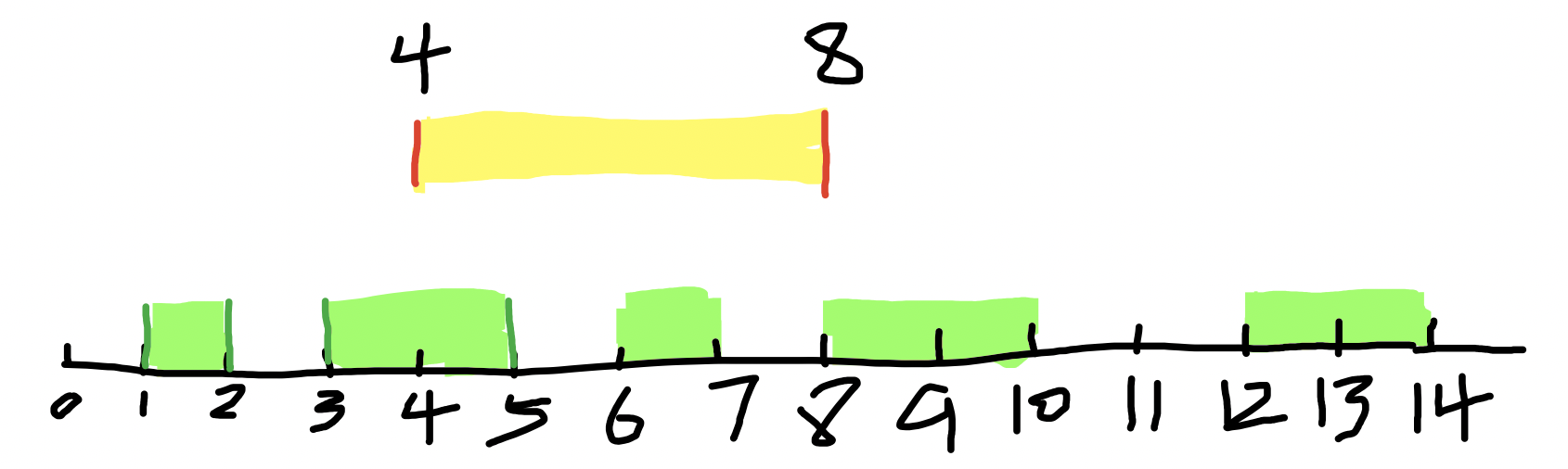
当前区间的右端点大于等于新区间的左端点，表明重叠，这时需要去看新区间的右端点，看看新区间一共将区间列表中的区间覆盖了多少，看看下面的图就懂我这句话的意思了。

看看上面的图，新区间的右端点8一直扩张到8-10区间，因此，当第一步到区间3-5停止后，只要当前区间的左端点小于等于新区间的右端点（表明重叠），就将新区间的左右端点进行更换（扩张新区间），至于更换规则，看图说话，左端点选择新区间左端点与当前区间的左端点较小值，右端点选择新区间右端点与当前区间右端点较大值。

更换过程：4-8 => 3-8 => 3-8 => 3-10

当目前区间到达12-13时，当前区间的左端点已经大于新区间右端点，表明不再重叠，直接加入结果集

代码

public int[][] insert(int[][] intervals, int[] newInterval) {
        int[][] res = new int[intervals.length + 1][2];
        int idx = 0;
        // 遍历区间列表：
        // 首先将新区间左边且相离的区间加入结果集
        int i = 0;
        while (i < intervals.length && intervals[i][1] < newInterval[0]) {
            res[idx++] = intervals[i++];
        }
        // 接着判断当前区间是否与新区间重叠，重叠的话就进行合并，直到遍历到当前区间在新区间的右边且相离，
        // 将最终合并后的新区间加入结果集
        while (i < intervals.length && intervals[i][0] <= newInterval[1]) {
            newInterval[0] = Math.min(intervals[i][0], newInterval[0]);
            newInterval[1] = Math.max(intervals[i][1], newInterval[1]);
            i++;
        }
        res[idx++] = newInterval;
        // 最后将新区间右边且相离的区间加入结果集
        while (i < intervals.length) {
            res[idx++] = intervals[i++];
        }

        return Arrays.copyOf(res, idx);
    }

关于bitset的使用

说了这么多，都没有用到bitset，肯定有人会说那开头讲这个是为了什么呢？？？别急，讲了的肯定都有用

区间合并的使用

实际上思路是很简单的，只需要将题目中给的区间列表依次用set的方法放入bitset中，完全放入后，再遍历bitset（当然是用nextSetBit和nextClearBit的方法啦～），使用nextSetBit的方法获取区间的左端点，nextClearBit的方法获取区间的右端点（有几个需要注意的点，在代码后面会解释）

public int[][] merge(int[][] intervals) {
    BitSet bitSet = new BitSet();
    int max = 0;
    for (int[] interval : intervals) {
        int temp = interval[1] * 2 + 1;
        bitSet.set(interval[0] * 2, temp, true);
        max = temp >= max ? temp : max;
    }

    int index = 0, count = 0;
    while (index < max) {
        int start = bitSet.nextSetBit(index);
        int end = bitSet.nextClearBit(start);

        int[] item = {start / 2, (end - 1) / 2};
        intervals[count++] = item;

        index = end;
    }
    int[][] ret = new int[count][2];
    for (int i = 0; i < count; i++) {
        ret[i] = intervals[i];
    }

    return ret;
}

注意点: 说好的是将区间放入bitset里，为什么代码里写的是将区间左端点乘2，右端点乘2加1放入bitset呢？原因很简单，我画个图你就明白了

假设有两个区间1-3和4-6，如果直接放入bitset，结果就是1,2,3,4,5,6全部都是true，然后合并区间时，会发现在bitset里无法区分这两个本来分离的区间，因此需要借助乘2来增加间距

结果就是如上图所示，最后放入bitset里的结果就是2,3,4,5,6,8,9,10,11,12，因此可以很清楚的利用nextSetBit(0) 获得2，nextClearBit(2)获得7，再对其进行之前为加间距做的操作的逆操作即可，同理，8-12也是一样

区间插入的使用

关于这种类型的使用，其实原理上与上面的是差不多的，也都是将所有的区间依次放入bitset，包括新区间，最后再进行区间合并与分离

代码如下：

public int[][] insert(int[][] intervals, int[] newInterval) {
    BitSet bitSet = new BitSet();

    int max = 0;
    for(int[] interval : intervals){
        int temp = 2*interval[1]+1;
        bitSet.set(2*interval[0],temp,true);
        max = max > temp ? max : temp;
    }

    bitSet.set(2*newInterval[0],2*newInterval[1]+1,true);
    max = max > 2*newInterval[1]+1 ? max : 2*newInterval[1]+1;

    int index = 0, count = 0;
    List<int[]> ret = new ArrayList<>();
    while(index < max){
        int start = bitSet.nextSetBit(index);
        int end = bitSet.nextClearBit(start);

        int[] item = {start/2,(end-1)/2};

        ret.add(item);
        count++;
        index = end;
    }
    int[][] ans = new int[count][2];
    for(int i=0;i<count;i++){
        ans[i] = ret.get(i);
    }

    return ans;
}

注意点与上面的是一样的，注意区间间距的分离

结束

以上就是关于区间问题的大体介绍了，按我的想法来看，只要是区间类的问题，都可以无脑使用bitset的方法来写，十有八九能AC（瞎猜的，别介意～）

至于这几天的番嘛，就快了，就快了～